WEEK2.2.1 多重特征量

多重特征量（变量）

前面所学的线性回归是一元的，即只有一个特征量x，考虑到预测房价这个模型，现实情况下需要多个变量。用$$x_1,x_2,...,x_n$$表示，而m仍为训练样本的数量。

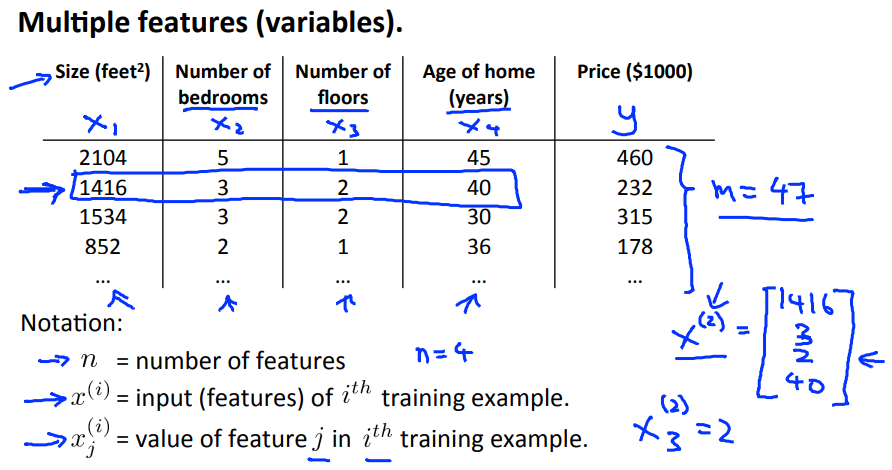
此时假设函数就会变成多元的形式。

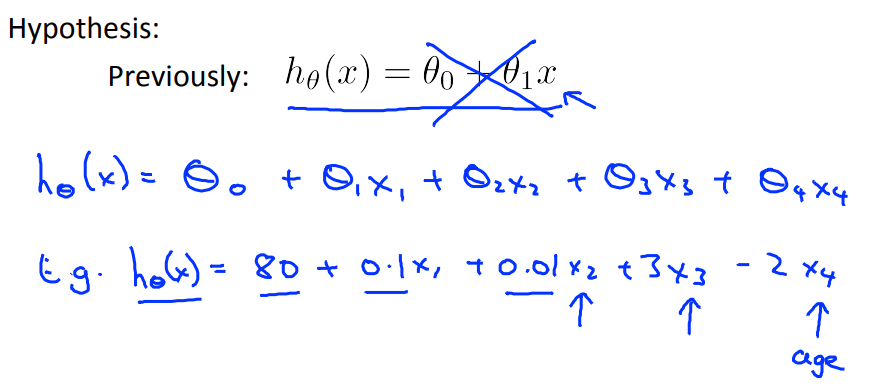
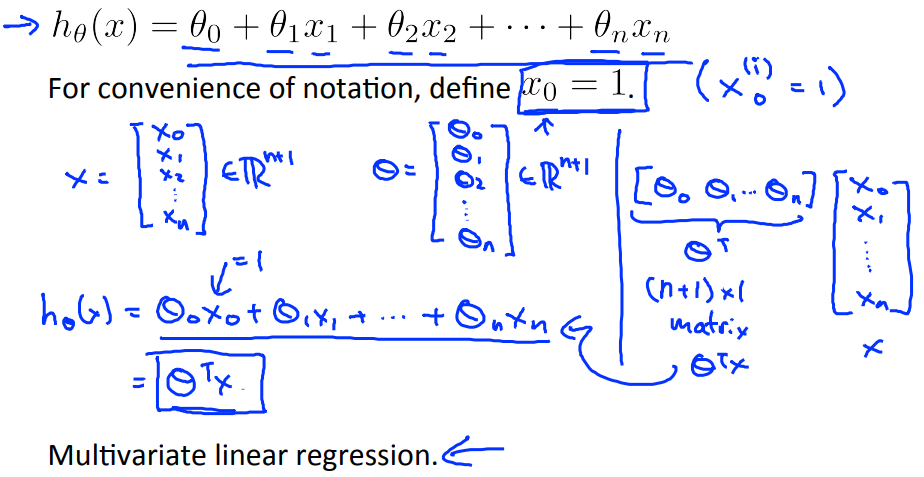
定义$$x_0=1$$，这样n个特征量就可以表示成n+1维向量$$x$$的形式，$${\theta }_0,...,{\theta }_n$$也可以表示成n+1维向量$$\theta$$，从而假设函数可以用向量乘法表示。

阅读材料

Multiple Features

Note: [7:25 - $${\theta }^T$$ is a 1 by (n+1) matrix and not an (n+1) by 1 matrix]

Linear regression with multiple variables is also known as "multivariate linear regression".

We now introduce notation for equations where we can have any number of input variables.

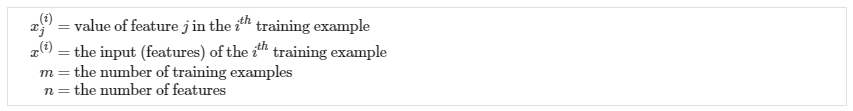
The multivariable form of the hypothesis function accommodating these multiple features is as follows:

$$h_{\theta }(x)={\theta }_0+{\theta }_1{x}_1+{\theta }_2{x}_2+{\theta }_3{x}_3+\cdots +{\theta }_n$$

In order to develop intuition about this function, we can think about $${\theta }_0$$ as the basic price of a house, $${\theta }_1$$ as the price per square meter, $${\theta }_2$$ as the price per floor, etc. $$x_1$$ will be the number of square meters in the house,$$x_2$$ the number of floors, etc.

Using the definition of matrix multiplication, our multivariable hypothesis function can be concisely represented as:

This is a vectorization of our hypothesis function for one training example; see the lessons on vectorization to learn more.

Remark: Note that for convenience reasons in this course we assume $$x_0^{(i)}=1\text{ for }(i\in 1,\dots ,m)$$. This allows us to do matrix operations with theta and x. Hence making the two vectors 'θ' and $$x^{(i)}$$ match each other element-wise (that is, have the same number of elements: n+1).]