WEEK1.6-Cost Function Intuition

用简化后的算法，即让这个函数只有一个参数\(\theta_1\),即设定\(\theta_0=0\)来理解代价函数。

这是我们上次所讲过的内容，我们想找一条直线来拟合我们的数据，所以我们用\(\theta_0\)\(\theta_1\)

等参数得到了假设，而且通过选择不同的参数，我们会得到不同的直线拟合。

通过利用简化的假设得到的代价函数，我们可以试着更好地理解代价函数这个概念，我们要理解的是这两个重要的函数代价函数和假设函数

\(h_\theta(x)\)和\(J(\theta_1)\),\(h_\theta(x)\)这个函数是假设函数，对于固定的\(\theta_1\),这是一个关于x的函数，假设函数就是一个关于x（房子大小）的函数，与此不同的是代价函数J是关于一个\(\theta_1\)的函数

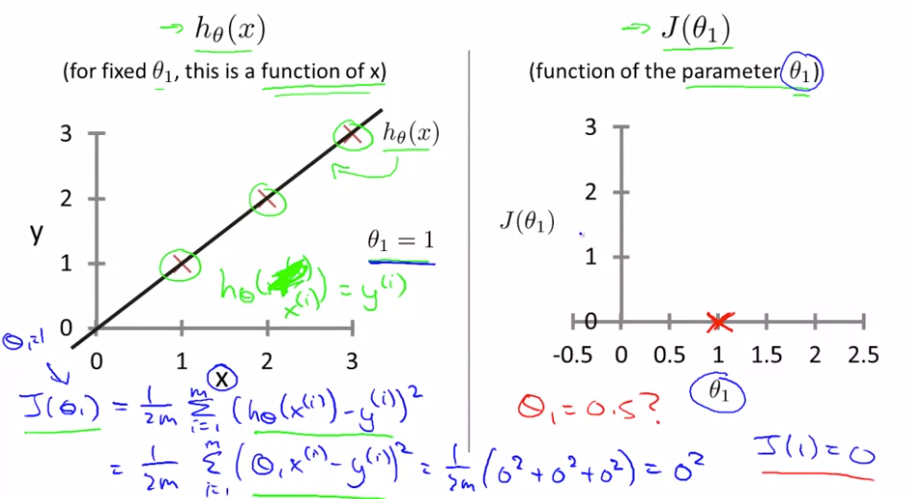
• 假设函数比如样本为(1,1)(2,2)(3,3),选择\(\theta_1\)等于1，则图像如下左图。这时当\(\theta_1\)等于1时\(J(\theta_1)\)等于多少？

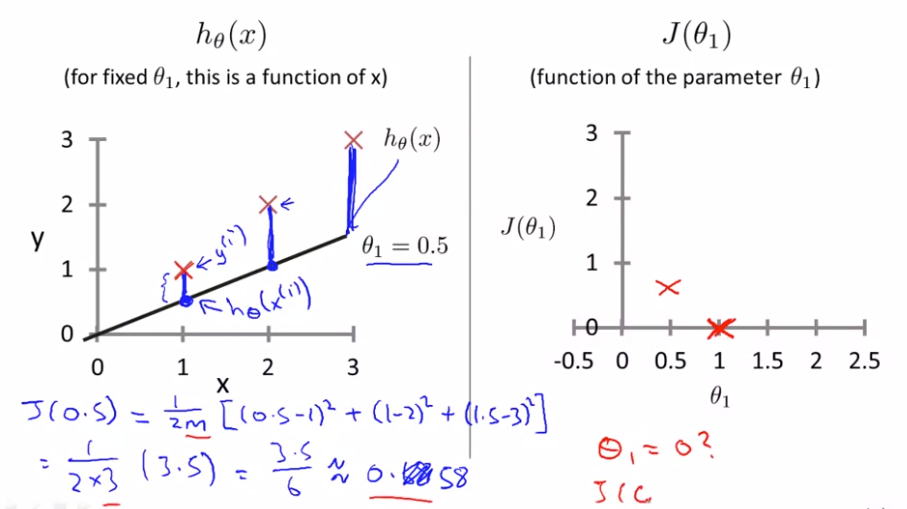
• 假设\(\theta_1=0.5\),则假设函数如下左图，\(J(\theta_1)=0.58\)

• 假设\(\theta_1=0\)，则假设函数如下左图,\(J(\theta_1)=14/6\)

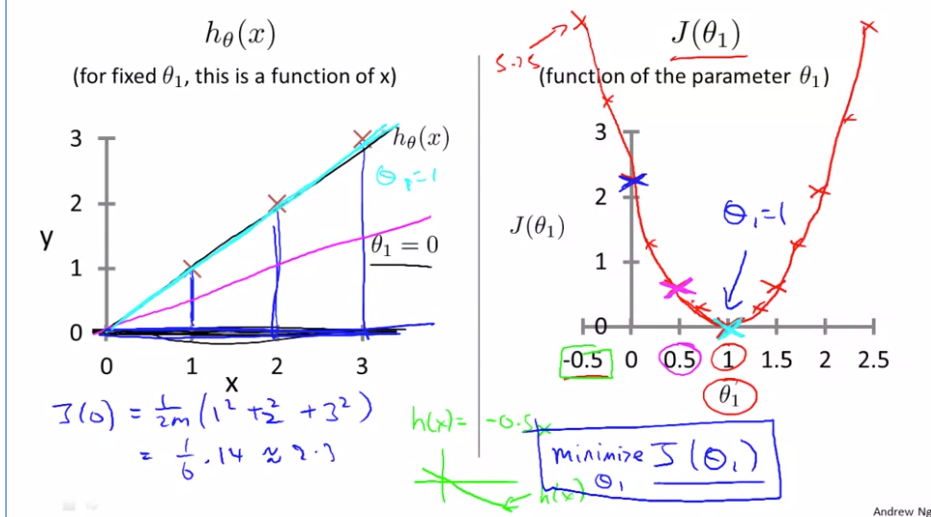
对于任意一个\(\theta_1\)的取值，我们会得到一个不同的\(J(\theta_1)\),而且我们可以利用这些来描出右边的这条曲线。学习算法的优化目标是找到一个\(\theta_1\)的值，来使\(J(\theta_1)\)最小化。对于上图\(J(\theta_1)\)最小化的值对应的\(\theta_1=1\)，这个就确实对应着最佳的通过了数据点的拟合直线。对于这个样本，我们最后能够完美地拟合。这就是为什么最小化\(J(\theta_1)\)对应着寻找一个最佳拟合直线的目标